¿Cómo convertir binario a decimal? - Ejemplos resueltos

¿Cómo convertir binario a decimal?

Binario es el tipo más simple de sistema numérico que usa solo dos dígitos de 0 y 1 (es decir, valor de base 2). Dado que la electrónica digital tiene solo estos dos estados (0 o 1), el número binario es el más preferido por los ingenieros informáticos modernos, los especialistas en redes y comunicaciones y otros profesionales.

Mientras que el número decimal es el sistema numérico más familiar para el público en general. Es la base 10 que tiene solo 10 símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. También puedes convertir binario a octal.

Conversión de sistema numérico binario a decimal

Existen principalmente dos métodos para convertir UN número binario en un número decimal: usar la notación posicional y usar la duplicación. Estos métodos se explican a continuación.

Uso de notación posicional

Dado que los números numéricos son un tipo de sistema numérico posicional. Eso significa que el peso de las posiciones de derecha a izquierda son como 20, 21, 22, 23 ... y así sucesivamente para la parte entera y el peso de las posiciones de izquierda a derecha son como 2-1, 2-2, 2-3, 2-4... y así sucesivamente para la parte fraccionaria.

Supongamos que cualquier número binario sin signo es bnb(n - 1) ... b1b0.b-1b - 2 ... b (m - 1)bm. Entonces el número decimal es igual a la suma de dígitos binarios (bn) multiplicada por su potencia de 2 (2n), es decir, bnb (n-1) ... b1b 0.b - 1b - 2 ... b(m-1) bm = bn x 2n + b (n-1) x 2 (n-1) + ... + b1 x 21 + b x 020 + b – 1 x 2 – 1 + b -22 – 2 + ...

Este es un algoritmo simple donde tienes que multiplicar el valor posicional de binario con su dígito y obtener la suma de estos pasos.

Ejemplo # 1

convertir el número binario 11001010 en un número decimal. Ya que aquí no hay punto binario ni parte fraccionaria. Asi que,

Binario a decimal es,

= (11001010)₂
= 1x2⁷ + 1x2⁶ + 0x2⁵ + 0x2⁴ + 1x2³ + 0x2² + 1x2¹ + 0x2⁰
= 128 + 64 + 0 + 0 + 8 + 0 + 2 + 0
= (202)₁₀

Ejemplo # 2

Convertir el número binario 1010.1011 en número decimal. Ya que aquí hay un punto binario con parte fraccionaria. Así que

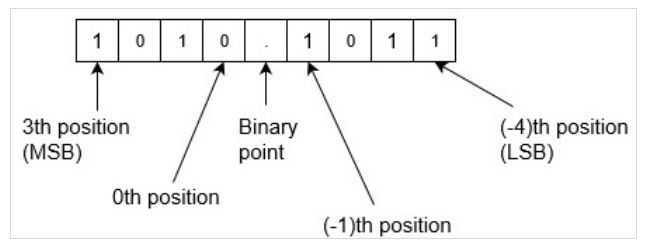
Binario a decimal es,

= (1010.1011)₂
= 1x2³ + 0x2² + 1x2¹ + 0x2⁰ + 1x2^-1 + 0x2^-2 + 1x2^-3 + 1x2^-4
= 8 + 0 + 2 + 0 + 0.5 + 0 + 0.125 + 0.0625
= (10.6875)₁₀

Uso de la duplicación

Este es un método simple para convertir un número binario en número decimal, debe comenzar desde el dígito más a la izquierda (o MSB) desde la entrada. Tome el bit más significativo (MSB), hacia abajo, luego multiplique por 2 con él y agregue el segundo bit más a la izquierda, guárdelo como resultado actual, luego nuevamente multiplique por 2 con el resultado actual y agregue el tercer bit más a la izquierda,

actualice este valor como resultado actual y siga hasta la adición de un bit menos significativo (LSB o bit más a la derecha). Dado que está duplicando (multiplicando por 2) cada vez, este método se conoce como Duplicación.También puedes convertir binario a hexadecimal.

Estos son algoritmos simples que se explican a continuación en pasos

• Anote el número binario.
• Comenzando desde la izquierda, duplique su total anterior y agregue el dígito actual.
• Duplica tu total actual y añade el siguiente dígito a la izquierda.
• Repita el paso anterior.

Por ejemplo,

convierta el número binario 11101110 en número decimal. De acuerdo con el algoritmo anterior, binario a decimal es,

= (11101110)₂
= 1
= 12 + 1 =3
= 32 + 1 = 7
= 72 + 0 = 14
= 142 + 1 = 29
= 292 + 1 = 59
= 592 + 1 = 119
= 1192 + 0 = 238
= (238)₁₀