En este artículo, echamos un vistazo a lo que son los sistemas numéricos decimales y binarias, cómo convertir números decimales a binarias y viceversa. También explicamos las matemáticas detrás de la conversión decimal-binaria y enumeramos programas simples en Java, JavaScript y Python para convertir números decimales a binarias.
Fondo
Los sistemas numéricos decimales y binarias son dos de los sistemas numéricos más utilizados en todo el mundo. El sistema decimal es el más familiar para nosotros y se usa en casi todas partes en nuestros cálculos diarios. Tiene una base de 10, es decir, 10 caracteres numéricos, o 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9.
Por otro lado, el sistema numérico binaria se usa ampliamente en la programación a nivel de máquina. Tiene una base de 2, es decir, dos caracteres numéricos: 0 y 1.
Casi todas las computadoras y dispositivos digitales funcionan con el sistema binaria, porque es muy fácil de implementar en circuitos electrónicos a través de puertas lógicas. En las computadoras, cada dígito de un número binaria se llama 'bit'. Por ejemplo:
- 10 es un número binaria de 2 bits, donde 1 y 0 son bits
- 110 es un número binaria de 3 bits
- 11011 es un número binaria de 5 bits
Existen varios métodos y programas para convertir números decimales a binarias y viceversa. Primero echemos un vistazo al método más común utilizado para la conversión y luego profundicemos en las matemáticas detrás de la conversión decimal-binaria.
Cómo Convertir Números Decimales a Binaria
Veamos dos casos: convertir enteros decimales a binaria y luego fracciones decimales menores que 1 a binaria.
Enteros Decimales a Binaria: Algoritmo
Paso 1. Divide el número entero por 2, mientras anotas el cociente y el resto.
Paso 2. Luego, divide el cociente nuevamente por 2 y registra el tercer cociente y el resto.
Paso 3. Así, sigue dividiendo cada cociente sucesivo por 2 hasta obtener un cociente de cero.
Paso 4. Después de esto, escribe todos los restos en orden inverso para obtener la representación binaria del entero.
Por ejemplo, vamos a convertir el entero 15 a binaria. Divide el número entero por 2 sucesivamente mientras anotas el cociente y el resto.
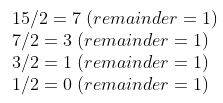
Luego, escribe todos los residuos en orden inverso. En este ejemplo, los residuos son 1, 1, 1, 1. Entonces, escribiendo en orden inverso, el número 15 en decimal se representa como 1111 en binaria.
Para un entero par, tomemos el ejemplo de 10.
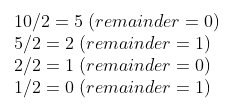
Entonces, el número decimal 10 se representa como 1010 en binaria.
De Fracciones Decimales a Binarias: Algoritmo
Para convertir una fracción a binaria, siga el proceso opuesto al descrito anteriormente.
Paso 1. Multiplique la fracción por 2, mientras anota las partes enteras y fraccionarias resultantes del producto.
Paso 2. Sigue multiplicando cada fracción resultante sucesiva por 2 hasta que obtengas un producto de fracción resultante de cero.
Paso 3. Ahora, escribe todas las partes enteras del producto en cada paso.
Por ejemplo, convertimos la fracción 0.625 a binaria. Multiplica la fracción por 2 sucesivamente mientras anotas las partes entera y fraccionaria del producto.
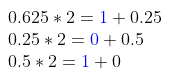
Vemos que las partes enteras resultantes del producto son 1, 0, 1. Por lo tanto, simplemente escríbalas después del punto decimal para obtener la notación binaria. Entonces, 0.625 se puede escribir como 0.101 en binaria.
Cómo Convertir Números Binarias a Decimal
Veamos dos casos: convertir enteros binarias a decimales y luego fracciones binarias a binarias.
De Enteros Binarias a Decimal: Algoritmo
Paso 1. Para convertir un entero binaria a decimal, comience agregando el dígito más a la izquierda a 0.
Paso 2. Luego, multiplique esto por 2 y agregue el siguiente dígito en su número (a medida que avanza de izquierda a derecha) a este producto. (En otras palabras, multiplicar el producto actual en cada paso por 2 y sumar el dígito actual).
Paso 3. Continúe este proceso hasta que no queden más dígitos.
Por ejemplo, vamos a convertir el entero binaria 1001 a decimal. Multiplique el total por 2 y agregue el dígito actual, comenzando desde la izquierda.
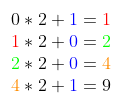
Por lo tanto, la conversión de binaria a decimal de 1001 es 9.
Fracciones Binarias a Decimal
Paso 1. Para convertir una fracción binaria a decimal, comience agregando el dígito más a la derecha a 0.
Paso 2. Luego, divida esto por 2, agregue el siguiente dígito a este total (mientras avanza de derecha a izquierda), y así sucesivamente.
Paso 3. Sigue haciendo esto hasta que no queden más dígitos.
Por ejemplo, vamos a convertir la fracción 0.1101 a decimal. Divide el total por 2 y suma el dígito actual, comenzando desde la derecha.
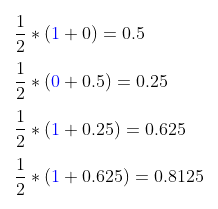
Como se ve, la representación decimal de 0.1101 es 0.8125.
Las Matemáticas Detrás De La Conversión Decimal-Binaria
Cualquier número en un sistema numérico se puede representar como su expansión base, donde 'base' es la base numérica, por ejemplo, la base 2 es binaria, la base 10 es decimal, la base 16 es hexadecimal, etc.
Entonces, cualquier número entero se puede representar de la siguiente manera:

Dónde,
a es un entero
x es el valor del dígito
b es el valor base
Por ejemplo, el número entero 694 se puede representar en base 10 y base 2 como:

Del mismo modo, una fracción puede ser como sigue:

Pónde,
A es una fracción
x es el valor del dígito
b es el valor base
Por ejemplo, la fracción 0. se puede representar en base 10 y base 2 como:

Representación binaria de números recurrentes y no terminales
Algunas fracciones que se pueden representar en el sistema decimal se encuentran con un flujo infinito de 0 y 1. Estas son las fracciones que, cuando se convierten a decimales en el sistema decimal, devuelven una secuencia infinitamente larga de dígitos después del punto. Por lo tanto, se llaman números que no terminan y que se repiten.
Por ejemplo, considere la fracción 1/6. El valor decimal de 1/6 es:

Vemos que el dígito '6' sigue repitiéndose después del período, hasta el infinito.
Esto se debe a que, para representar finitamente cualquier número dado en un sistema de base n, el denominador de ese número debe ser una potencia de la base (b). En el ejemplo anterior, 6 no es una potencia de 10, por lo que 1/6 no se puede representar en el sistema de base 10 en formato decimal.
De manera similar, aquellos números con un denominador que no son una potencia de 2 no pueden representarse finitamente en el sistema de base 2.
Por ejemplo, considere 0.3. 0,3 = 3/10. Dado que 10 no es una potencia de 2, 0,3 no se puede representar en el sistema de base 2.

Vemos que los 4 dígitos '1001' se siguen repitiendo después del punto decimal hasta el infinito. Por lo tanto, podemos representarlo como:

Tabla Decimal a Binaria
Aquí hay una práctica tabla de conversión decimal-binaria:
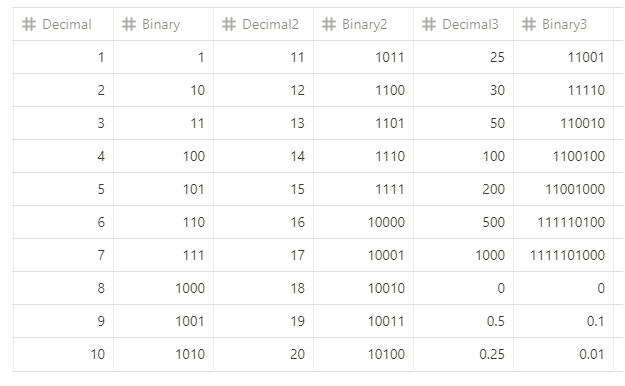
Programas Para Convertir Decimal A Binaria
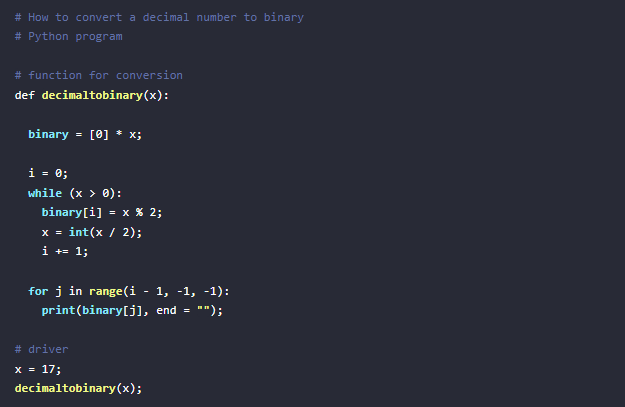
Aquí hay un ejemplo de programas para convertir números decimales a números binarias. La lógica utilizada es prácticamente la misma para ambos: Java y Python.
De Decimal A Binaria En Java
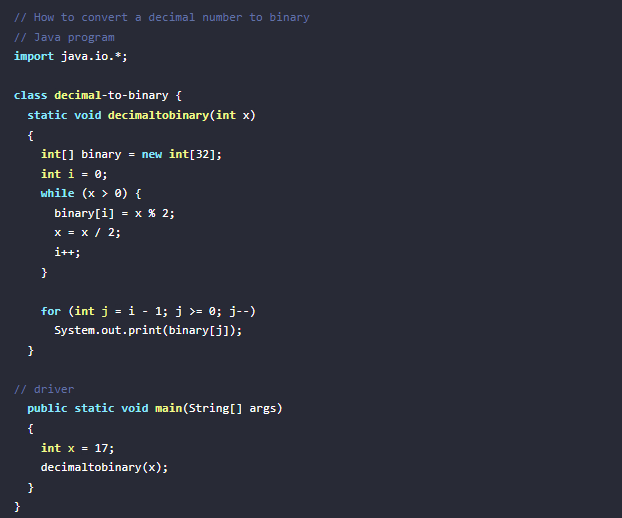
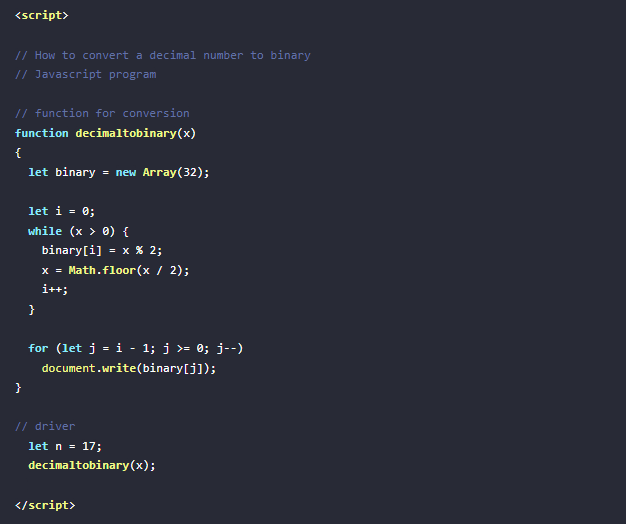
De Decimal a Binaria en Javascript
De Decimal a Binaria en Python